로지스틱 회귀(Logistic Regression)

by

1. 개요

로지스틱 회귀(Logistic Regression)는 종속 변수가 범주형(categorical)일 때 사용하는 지도 학습(Supervised Learning) 알고리즘입니다. 특히 이진 분류(Binary Classification) 문제에서 널리 사용됩니다. 예를 들면, 고객이 상품을 구매할지(1) 안 할지(0), 이메일이 스팸(1)인지 아닌지(0) 등을 예측할 때 사용됩니다.

2. 선형 회귀와의 차이점

  • 선형 회귀(Linear Regression)는 연속적인 값을 예측하는 반면, 로지스틱 회귀는 범주형 결과(예: 0 또는 1)를 예측합니다.
  • 선형 회귀에서는 결과가 직선 형태로 출력되지만, 로지스틱 회귀는 시그모이드 함수(Sigmoid Function) 를 사용하여 출력을 확률 값(0과 1 사이)으로 변환합니다.

3. 시그모이드 함수(Sigmoid Function)

로지스틱 회귀의 핵심은 시그모이드 함수(로지스틱 함수)를 사용하는 것입니다. 시그모이드 함수는 다음과 같이 정의됩니다.

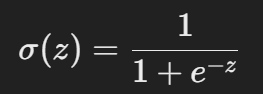
여기서 zzz는 입력 변수 XXX 에 대한 선형 결합:

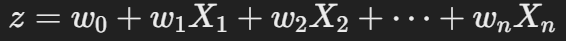
시그모이드 함수의 특징:

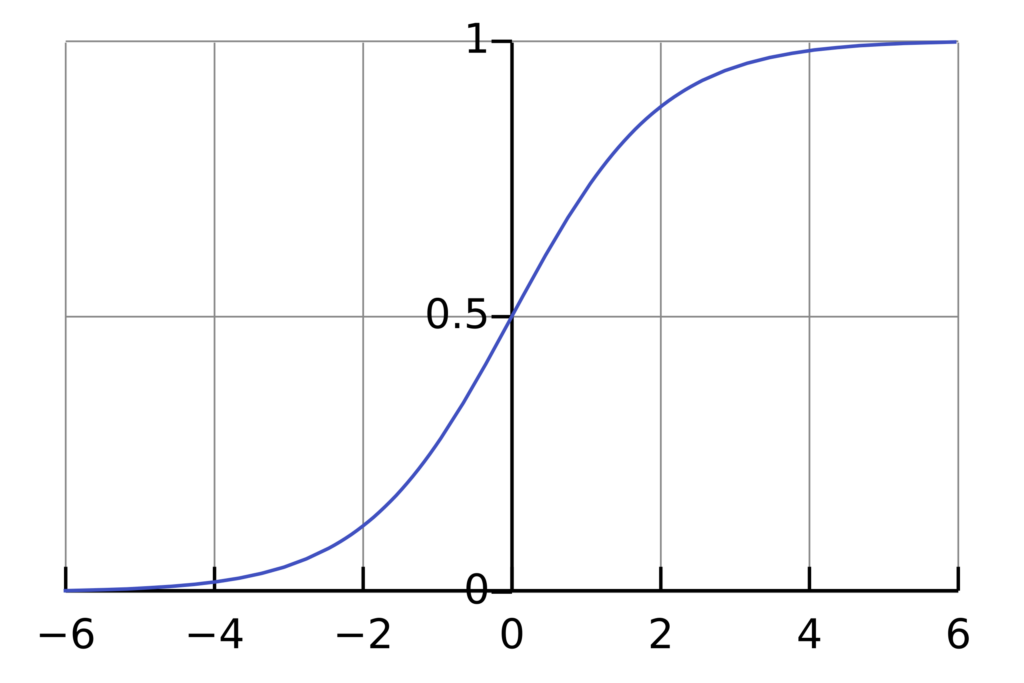
  • zzz 값이 매우 작으면 (−∞), 출력값은 0에 가깝습니다.
  • zzz 값이 매우 크면 (+∞), 출력값은 1에 가깝습니다.
  • z=0z = 0z=0 일 때, 출력값은 0.5가 됩니다.

4. 확률과 결정 경계

로지스틱 회귀의 출력값은 0~1 사이의 확률을 나타내며, 일반적으로 임계값(threshold) 0.5를 기준으로 분류됩니다.

  • P(Y=1∣X) ≥ 0.5P → 1로 분류
  • P(Y=1∣X) < 0.5P → 0으로 분류

5. 비용 함수(Cost Function)

선형 회귀에서는 평균제곱오차(MSE)를 사용하지만, 로지스틱 회귀에서는 로그 손실(Log Loss) 또는 이진 크로스 엔트로피(Binary Cross-Entropy) 를 비용 함수로 사용합니다.

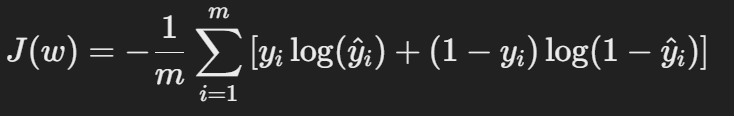
여기서,

  • yiy_iyi​ : 실제값 (0 또는 1)
  • y^i\hat{y}_iy^​i​ : 예측 확률값 (시그모이드 함수 출력)

이 비용 함수는 오차가 커질수록 손실 값이 증가하며, 최적의 가중치 www 를 찾기 위해 경사 하강법(Gradient Descent) 을 사용하여 최소화합니다.

6. 다중 클래스 분류(Multiclass Classification)

기본적인 로지스틱 회귀는 이진 분류(Binary Classification)에 적합하지만, 다중 클래스(Multiclass Classification) 문제에서는 아래와 같은 확장 방법을 사용합니다.

  1. 일대다(One-vs-All, OvA): 각 클래스를 하나의 이진 분류 문제로 변환하여 여러 개의 로지스틱 회귀 모델을 학습시킵니다.
  2. 소프트맥스 회귀(Softmax Regression, 다항 로지스틱 회귀): 다중 클래스 문제를 확률 분포 형태로 변환하는 소프트맥스 함수를 적용하여 직접 다중 클래스를 예측합니다.

7. 로지스틱 회귀의 장점

  • 결과가 확률 값으로 해석 가능
  • 계산 비용이 상대적으로 낮음
  • 해석이 쉬워 모델 설명 가능성(Interpretability)이 높음
  • 과적합 방지를 위해 L1 (Lasso), L2 (Ridge) 정규화 적용 가능

8. 로지스틱 회귀의 단점

  • 선형적 관계를 가정하므로 복잡한 비선형 문제에는 적합하지 않음
  • 이상치(Outlier)에 민감함
  • 특성 변수가 많아지면 성능이 저하될 수 있음

9. 파이썬을 이용한 구현 예제

아래는 Python의 sklearn 라이브러리를 이용한 간단한 로지스틱 회귀 구현 예제입니다.

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

# 예제 데이터 (사이킷런의 데이터셋 활용)
from sklearn.datasets import load_breast_cancer
data = load_breast_cancer()
X, y = data.data, data.target

# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 로지스틱 회귀 모델 생성 및 학습
model = LogisticRegression(max_iter=1000)
model.fit(X_train, y_train)

# 예측 및 정확도 평가
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"모델 정확도: {accuracy:.4f}")

10. 결론

로지스틱 회귀는 이진 및 다중 클래스 분류 문제에서 널리 사용되는 기법으로, 특히 해석이 용이하고 계산이 빠른 모델입니다. 하지만 복잡한 비선형 관계를 처리하는 데는 한계가 있어 의사결정나무(Decision Tree), 랜덤 포레스트(Random Forest), 신경망(Neural Networks) 과 같은 모델과 비교하여 적절한 상황에서 활용하는 것이 중요합니다.

Leave a Comment