차원 축소(Dimensionality Reduction)는 고차원의 데이터를 저차원의 공간으로 변환하는 기법입니다. 이는 데이터의 중요한 정보를 최대한 유지하면서 불필요한 정보(노이즈)를 제거하고, 계산 효율성을 높이며, 데이터 시각화와 모델 성능 향상에 기여합니다.
1. 차원 축소의 필요성
(1) 고차원의 저주(Curse of Dimensionality)
- 데이터 차원이 증가하면 샘플 간 거리가 멀어지고, 학습 성능이 저하됨
- 데이터가 희소(Sparse)해지면서 클러스터링과 분류 모델의 성능이 떨어질 수 있음
(2) 연산 속도 및 저장 공간 절감
- 머신러닝 모델에서 데이터 차원이 많을수록 연산 비용이 증가
- 데이터 차원을 줄이면 연산량 감소 및 모델 학습 속도 향상
(3) 노이즈 제거 및 과적합(Overfitting) 방지
- 고차원 데이터에서 불필요한 특징을 제거하여 모델의 일반화 성능을 높임
- 차원 축소를 통해 의미 없는 변수들을 줄이면 모델이 더 중요한 패턴을 학습
(4) 데이터 시각화 가능
- 데이터를 2D 또는 3D로 변환하여 패턴과 군집 구조를 직관적으로 이해할 수 있음
2. 차원 축소 기법
차원 축소는 크게 “특징 선택(Feature Selection)” 과 “특징 추출(Feature Extraction)” 방식으로 나뉩니다.
(1) 특징 선택(Feature Selection)
- 기존의 특징(Feature) 중 일부만 선택하여 차원을 줄이는 방법
- 대표적인 방법:
- Filter Method: 변수 간 상관관계, 분산, 상호정보 등을 기반으로 중요한 특징 선택 (e.g., 카이제곱 검정, 분산 임계값)
- Wrapper Method: 머신러닝 모델을 사용하여 최적의 특징 조합을 탐색 (e.g., Recursive Feature Elimination)
- Embedded Method: 모델 학습 과정에서 중요한 특징을 자동으로 선택 (e.g., LASSO Regression)
(2) 특징 추출(Feature Extraction)
기존의 특징을 변환하여 새로운 특징을 생성하는 방법으로, 차원의 감소 효과가 큼
(a) 선형 차원 축소 기법
1) 주성분 분석(PCA, Principal Component Analysis)
- 데이터의 분산을 최대한 유지하는 새로운 축(주성분, Principal Component)을 생성
- 공분산 행렬을 고유값 분해(Eigendecomposition)하여 주요 성분을 추출
- 고차원 데이터를 몇 개의 주성분으로 변환하여 차원 축소 수행
✔ 수학적 원리
- 데이터 행렬 XXX의 공분산 행렬 CCC를 계산:
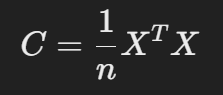
- CCC의 고유값과 고유벡터를 구하여 가장 큰 고유값에 해당하는 고유벡터(주성분)를 선택
✔ 장점
- 계산 속도가 빠르고 데이터의 분산을 보존
- 비지도 학습(unsupervised learning) 방식으로 데이터 레이블이 필요 없음
✔ 단점
- 선형 변환만 가능하여 비선형 데이터에는 부적절
2) 선형 판별 분석(LDA, Linear Discriminant Analysis)
- 지도 학습 방식으로 클래스 간 분리를 최대화하는 방식으로 차원 축소
- PCA와 달리 레이블 정보(클래스)를 활용하여 중요한 축을 선택
✔ 수학적 원리
- 클래스 간 분산(SBS_BSB)과 클래스 내 분산(SWS_WSW)을 계산:
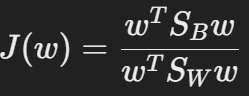
- 최적의 방향 벡터 www를 찾음
✔ 장점
- 분류 문제에서 성능 향상 가능
✔ 단점
- 데이터가 정규분포를 따른다고 가정
3) 특이값 분해(SVD, Singular Value Decomposition)
- PCA와 유사하지만 행렬 분해 방식을 활용하여 차원 축소
- 행렬 AAA를 세 개의 행렬로 분해: A=UΣVTA = U \Sigma V^TA=UΣVT
- 상위 kkk개의 특이값(Singular Value)만 선택하여 차원을 축소
✔ 응용 분야
- 자연어 처리(NLP)에서 잠재 의미 분석(LSA, Latent Semantic Analysis)에 활용
(b) 비선형 차원 축소 기법
1) t-SNE (t-Distributed Stochastic Neighbor Embedding)
- 비슷한 데이터 포인트는 가까이, 다른 데이터 포인트는 멀리 배치하여 저차원 표현 생성
- 높은 차원에서 유사한 점들을 2D 또는 3D 공간에서도 유사하게 배치
✔ 장점
- 비선형 데이터 구조를 잘 보존하며 시각화에 강점
✔ 단점
- 계산량이 많아 대규모 데이터셋에 부적절
2) UMAP (Uniform Manifold Approximation and Projection)
- t-SNE보다 빠르면서도 데이터의 전체 구조를 더 잘 유지하는 차원 축소 기법
- 위상수학을 활용하여 데이터 구조를 보존
✔ 장점
- t-SNE보다 연산 속도가 빠르고 군집 유지력이 뛰어남
3) 자동 인코더(Autoencoder)
- 인공 신경망을 활용한 차원 축소 기법
- 입력 데이터를 인코더(Encoder)로 축소하고, 디코더(Decoder)로 복원하면서 중요한 특징을 학습
✔ 구성
- 인코더(Encoder): 입력을 저차원 벡터로 압축
- 디코더(Decoder): 저차원 벡터를 원본 데이터로 복원
✔ 장점
- 복잡한 비선형 패턴을 학습 가능
- PCA보다 강력한 표현 학습이 가능
✔ 단점
- 신경망 훈련이 필요하여 계산량이 많음
3. 차원 축소 기법 비교
| 기법 | 유형 | 선형/비선형 | 장점 | 단점 |
|---|---|---|---|---|
| PCA | 비지도 | 선형 | 계산 속도 빠름, 분산 유지 | 비선형 데이터에 부적절 |
| LDA | 지도 | 선형 | 분류 성능 향상 | 클래스 간 관계를 반영 못할 수 있음 |
| SVD | 비지도 | 선형 | NLP에서 유용 | 데이터 복원력이 낮을 수 있음 |
| t-SNE | 비지도 | 비선형 | 시각화 성능 우수 | 연산량 많음 |
| UMAP | 비지도 | 비선형 | 빠르고 군집 유지력 우수 | 매개변수 튜닝 필요 |
| Autoencoder | 비지도 | 비선형 | 비정형 데이터에 강함 | 신경망 훈련 필요 |
4. 결론
차원 축소는 데이터 분석과 머신러닝 모델의 성능 향상에 중요한 역할을 합니다. 데이터 특성과 목적에 따라 적절한 기법을 선택하는 것이 핵심입니다.
- 데이터 압축 및 속도 향상 → PCA, SVD
- 분류 성능 향상 → LDA
- 시각화 → t-SNE, UMAP
- 복잡한 패턴 학습 → Autoencoder
적절한 차원 축소 기법을 선택하여 데이터 처리 효율성을 높이는 것이 중요합니다. 🚀
