68-95-99.7 규칙 (Three Sigma Rule)

by

68-95-99.7 규칙 (Three Sigma Rule)

68-95-99.7 규칙은 정규분포(Gaussian distribution)에서 평균(μ)과 표준편차(σ)를 기준으로 데이터가 분포하는 비율을 나타내는 경험적인 법칙입니다.

1. 규칙의 의미

정규분포에서 데이터가 평균을 중심으로 특정 시그마(σ) 범위 내에 포함될 확률은 다음과 같습니다.

시그마 범위포함 확률설명
±1σ68.3%전체 데이터의 68.3%가 평균(μ)에서 ±1표준편차(σ) 내에 위치
±2σ95.4%전체 데이터의 95.4%가 평균(μ)에서 ±2표준편차(σ) 내에 위치
±3σ99.7%전체 데이터의 99.7%가 평균(μ)에서 ±3표준편차(σ) 내에 위치

즉, 데이터가 정규분포를 따른다면, 평균을 중심으로 대부분의 값이 ±3σ 범위 내에 분포한다는 것을 의미합니다.

2. 시각적 이해 (정규분포 곡선)

정규분포를 나타내는 종형 곡선(Bell Curve)에서 평균을 중심으로 데이터가 퍼지는 방식은 다음과 같습니다.

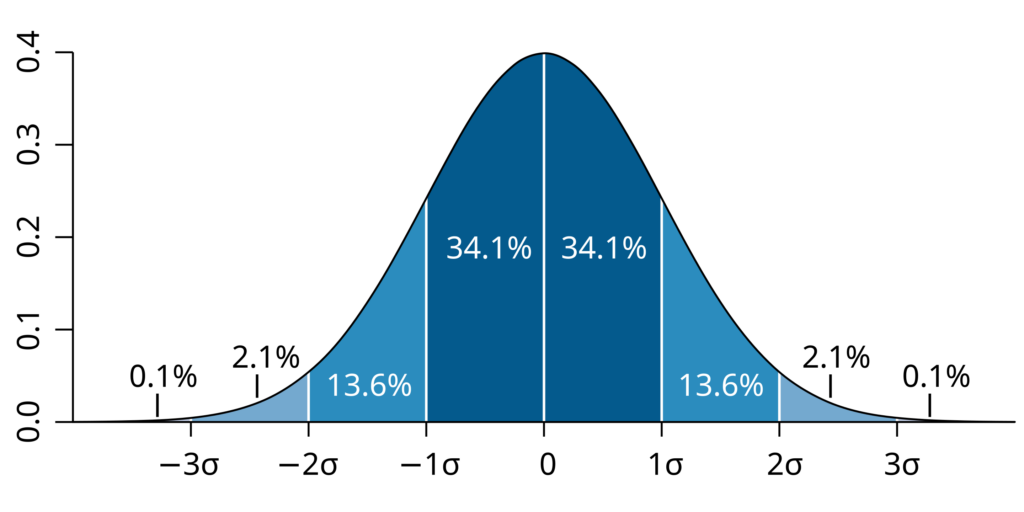
diff코드 복사μ - 3σ  |  μ - 2σ  |  μ - 1σ  |   μ   |  μ + 1σ  |  μ + 2σ  |  μ + 3σ
--------|----------|----------|--------|----------|----------|---------
  0.15% |   2.35%  |   13.59% | 34.13% |  13.59%  |   2.35%  |   0.15%

이때:

  • 68.3%의 데이터는 ±1σ 범위 내 존재
  • 95.4%의 데이터는 ±2σ 범위 내 존재
  • 99.7%의 데이터는 ±3σ 범위 내 존재
  • ±3σ를 벗어나는 값은 약 0.3% (즉, 이상치로 간주됨)

3. 활용 사례

✅ 품질 관리 (Six Sigma)

  • 제품 품질을 관리할 때, ±3σ를 벗어나는 결함률이 0.3% 이하로 유지되도록 목표 설정.
  • Six Sigma에서는 ±6σ까지 고려하여 결함률을 100만 개 중 3.4개로 줄이는 것을 목표로 함.

✅ 통계 분석 및 연구

  • ±2σ 범위를 사용하여 95% 신뢰구간을 설정하고, 가설 검정에서 데이터가 정상 범위에 있는지 판단.
  • ±3σ 이상 벗어난 데이터는 이상치(outlier)로 간주 가능.

✅ 리스크 관리 및 금융

  • 주식 시장 변동성 분석에서 ±2σ를 넘으면 비정상적인 시장 변동으로 판단.
  • 금융 포트폴리오에서 리스크 평가에 사용.

✅ 의학 및 생명과학

  • 환자의 건강 지표(예: 혈압, 혈당)가 ±2σ 범위 내에 있는지를 확인하여 정상 여부 평가.
  • ±3σ를 벗어나면 **특이 사례(rare event)**로 간주.

4. 핵심 요약

  • 68% → ±1σ 안에 존재 (대부분의 데이터)
  • 95% → ±2σ 안에 존재 (대부분의 정상적인 값)
  • 99.7% → ±3σ 안에 존재 (거의 모든 데이터)
  • ±3σ를 벗어난 값은 극히 드물고 이상치(outlier)로 판단 가능

즉, 68-95-99.7 규칙은 정규분포에서 데이터가 퍼져 있는 형태를 이해하고, 이상값을 탐지하며, 품질 관리를 위한 중요한 기준으로 활용됩니다.

Leave a Comment