PCA(Principal Component Analysis)

by

1. PCA란?

PCA(Principal Component Analysis)는 데이터의 차원을 축소하면서도 데이터의 분산을 최대한 보존하는 기법입니다. 즉, 고차원 데이터를 저차원으로 변환하여 주요 정보만 유지하면서 계산 비용을 줄이고, 데이터의 시각화를 돕는 데 사용됩니다.

2. PCA의 원리

PCA는 고차원 데이터를 저차원의 공간으로 투영하면서 중요한 정보(분산이 큰 방향)를 유지합니다. 이를 위해 다음 단계를 수행합니다.

3. PCA 알고리즘 단계

1) 데이터 정규화 (Normalization)

  • PCA를 수행하기 전에 데이터의 스케일을 맞추는 것이 중요합니다. 각 특성(feature)이 서로 다른 범위를 가지면, 특정 특성이 PCA 결과에 더 큰 영향을 줄 수 있기 때문입니다.
  • 보통 평균을 0, 분산을 1로 정규화(Standardization)합니다.
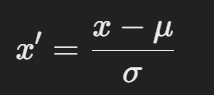
    • x : 원본 데이터 값
    • μ : 해당 특성의 평균
    • σ : 해당 특성의 표준편차

2) 공분산 행렬 계산

  • 각 특성 간의 관계를 분석하기 위해 공분산 행렬을 계산합니다.
  • 공분산 행렬은 데이터의 분산과 특성 간의 상관관계를 나타냅니다.
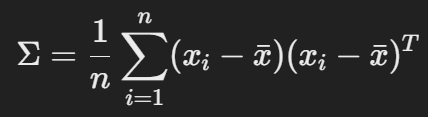
  • xi​는 개별 데이터 샘플,
  • xˉ는 각 특성의 평균 벡터,
  • Σ는 공분산 행렬입니다.

3) 고유값(Eigenvalues) 및 고유벡터(Eigenvectors) 계산

  • 공분산 행렬을 고유값 분해(Eigendecomposition)하여 고유값(eigenvalues)과 고유벡터(eigenvectors) 를 구합니다.
  • 고유값은 데이터의 분산을 설명하는 값이고, 고유벡터는 새로운 축을 형성합니다.
  • 여기서,
    • v는 고유벡터 (주성분),
    • λ는 고유값 (분산의 크기)입니다.
  • 고유값이 클수록 해당 고유벡터가 설명하는 분산이 크므로, 큰 고유값을 가지는 고유벡터들이 데이터의 주요 정보를 담고 있습니다.

4) 주성분 선택

  • 고유값이 큰 순서대로 정렬하여 상위 k개의 주성분을 선택합니다.
  • 데이터의 분산을 충분히 설명하는 누적 설명 분산 비율(Cumulative Explained Variance Ratio) 을 보고 적절한 k를 선택합니다.
  • ​​보통 누적 설명 분산 비율이 90%~95% 이상이 되도록 주성분을 선택합니다.

5) 데이터 변환 (차원 축소)

  • 선택한 k개의 주성분으로 원본 데이터를 변환합니다.
  • 데이터 행렬 XXX에 주성분 행렬(고유벡터 행렬) Vk​를 곱하여 차원 축소된 데이터를 얻습니다.
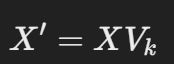
  • 여기서,
    • X : 원본 데이터 행렬 (정규화된 형태)
    • Vk​ : 선택된 k개의 주성분(고유벡터) 행렬
    • X′ : 변환된 k-차원 데이터

4. PCA의 장점과 단점

장점

  • 데이터의 차원을 효과적으로 축소하여 계산량을 줄일 수 있음.
  • 데이터의 분산을 유지하면서 노이즈를 제거하고 학습 성능을 향상시킬 수 있음.
  • 시각화(2D, 3D 변환) 에 유용함.

단점

  • 선형 변환을 기반으로 하므로 비선형적인 구조를 반영하지 못함.
  • 해석이 어려울 수 있음 (축소된 차원이 기존 특성과 직접적인 연관이 없을 수 있음).
  • 주성분을 선택하는 과정에서 중요한 정보가 손실될 가능성이 있음.

5. PCA 적용 예시 (Python 코드)

아래는 PCA를 활용한 차원 축소 예제입니다.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris

# 데이터 로드
data = load_iris()
X = data.data  # 특성 데이터

# 데이터 정규화
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# PCA 적용 (2차원으로 축소)
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

# 변환된 데이터 시각화
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=data.target, cmap='viridis', alpha=0.7)
plt.xlabel("Principal Component 1")
plt.ylabel("Principal Component 2")
plt.title("PCA 결과 (Iris 데이터)")
plt.colorbar(label="Target Label")
plt.show()

# 설명된 분산 비율 확인
print("Explained Variance Ratio:", pca.explained_variance_ratio_)

6. PCA의 응용 분야

  1. 데이터 시각화 : 고차원 데이터를 2D/3D로 변환하여 시각적으로 분석 가능.
  2. 차원 축소 : 모델의 성능을 유지하면서 학습 속도를 향상.
  3. 노이즈 제거 : 데이터에서 주요 정보만 유지하고 불필요한 요소 제거.
  4. 이미지 압축 : 주요 특징만 추출하여 저장 공간 절약.
  5. 금융 데이터 분석 : 주식 가격, 리스크 요인 등의 요약 분석.

7. PCA 확장 기법

  • Kernel PCA : 비선형 데이터에 적용하기 위해 커널 기법 사용.
  • Sparse PCA : 희소성 제약을 적용하여 해석 가능성 개선.
  • Incremental PCA : 대규모 데이터셋에서 배치 학습을 활용.

8. 결론

PCA는 데이터의 주요 특징을 유지하면서 차원을 줄이는 강력한 기법입니다. 특히, 데이터 분석과 머신러닝 모델의 성능을 최적화하는 데 유용합니다. 하지만 비선형 데이터에 대한 한계가 있으므로, 필요에 따라 Kernel PCA 등의 변형 기법을 활용할 수 있습니다.

Leave a Comment