자기조직화 지도(SOM, Self-Organizing Map) 군집 분석 기법
1. SOM 개요
자기조직화 지도(SOM, Self-Organizing Map)는 인공신경망(Artificial Neural Network, ANN)의 한 종류로, 데이터의 고차원 정보를 저차원의 격자로 정리하는 비지도 학습(unsupervised learning) 방식의 군집 분석 기법입니다.
- 1982년 핀란드의 Teuvo Kohonen이 개발한 알고리즘
- 고차원의 데이터를 저차원의 격자형 공간(Grid Space) 으로 맵핑
- 신경망이 데이터의 패턴을 스스로 학습(Self-Organizing) 하는 방식
- 주로 데이터 시각화, 군집 분석, 차원 축소 등에 사용
2. SOM(Self-Organizing Map)의 구성 요소
SOM은 인공 신경망 기반의 군집 분석 기법으로, 데이터의 고차원 구조를 저차원 격자로 변환합니다. SOM의 주요 구성 요소는 다음과 같습니다.
(1) 입력층(Input Layer)
- 입력 데이터 벡터를 받는 층
- 입력 벡터의 차원은 고차원(예: RGB 이미지의 경우 3차원)
- 각 뉴런과 연결된 가중치 벡터 존재
(2) 경쟁층(Competitive Layer)
- 격자(Grid) 형태의 뉴런(Neuron)으로 구성 (일반적으로 2D 격자)
- 각 뉴런은 가중치 벡터를 가짐 (입력 데이터의 차원과 동일)
- BMU(Best Matching Unit): 입력 벡터와 가장 유사한 가중치를 가진 뉴런
- 경쟁 과정에서 BMU를 찾고, 이웃 뉴런을 업데이트함
(3) 가중치(Weight)
- 뉴런이 입력 데이터를 표현하는 특징 벡터
- 학습 과정에서 가중치가 점진적으로 조정됨
- 초기에는 랜덤하게 설정되며 학습을 통해 데이터 패턴을 반영
(4) 이웃 함수(Neighborhood Function)
- BMU 주변 뉴런들도 가중치가 업데이트됨
- 일반적으로 가우시안 함수(Gaussian Function) 또는 메트릭 거리(Euclidean Distance) 사용
- 시간에 따라 이웃의 범위가 줄어들며 지역 최적화 진행
(5) 학습률(Learning Rate)
- 초기 학습률(α)은 비교적 크며, 점점 감소
- 가중치 업데이트 공식: Wnew=Wold+α⋅(X−Wold)W_{new} = W_{old} + \alpha \cdot (X – W_{old})Wnew=Wold+α⋅(X−Wold)
- WWW : 뉴런 가중치 벡터
- XXX : 입력 벡터
- α\alphaα : 학습률
3. SOM의 동작 원리
SOM은 입력 벡터들을 2D 또는 3D의 격자로 변환하면서 비슷한 특징을 가진 데이터들이 가까운 위치에 배치되도록 학습합니다.
- 초기화(Initialization)
- SOM 격자의 뉴런(Neuron)들을 랜덤한 가중치로 초기화
- 경쟁 단계(Competition Phase)
- 입력 벡터와 모든 뉴런 간 유클리드 거리(Euclidean Distance) 계산
- 가장 가까운 뉴런(BMU, Best Matching Unit)을 선택
- 협력 단계(Cooperation Phase)
- BMU를 중심으로 인접한 뉴런들에도 영향을 줌
- 가우시안 함수 기반의 이웃함수(Neighborhood Function) 를 사용하여 조정
- 적응 단계(Adaptation Phase)
- 선택된 뉴런과 주변 뉴런들의 가중치를 업데이트
- 가중치 조정 식: Wnew=Wold+α(X−Wold)W_{new} = W_{old} + \alpha (X – W_{old})Wnew=Wold+α(X−Wold) 여기서,
- WWW : 뉴런의 가중치
- α\alphaα : 학습률 (시간에 따라 감소)
- XXX : 입력 데이터
- 반복(iteration)
- 위 과정을 여러 번 반복하면서 학습
4. SOM의 특징
✅ 비지도 학습(unsupervised learning)
✅ 고차원 데이터의 차원 축소 가능
✅ 데이터의 군집 형성(clustering)이 직관적으로 가능
✅ 데이터의 시각화 및 패턴 분석 용이
✅ 지도 기반 데이터 표현으로 해석이 쉬움
💻구성도
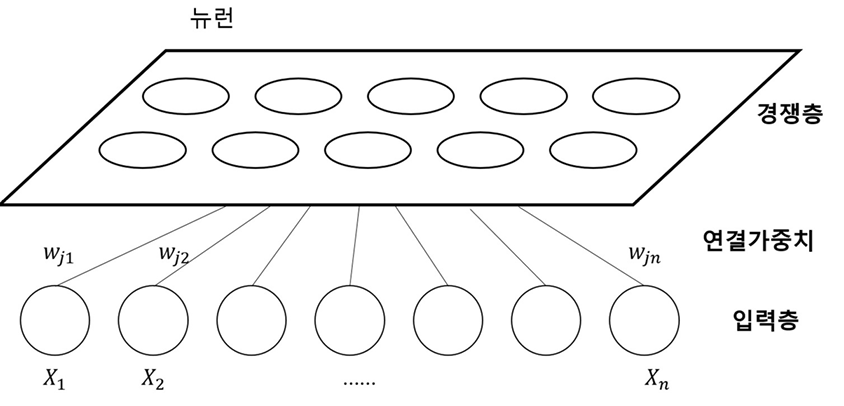
입력층과 경쟁층으로 구성되며, 경쟁층의 뉴런들이 2차원 격자 구조로 배열되어 고차원 입력데이터를 저차원공간에 시각적으로 표현하는 구조
5. SOM의 활용 분야
- 패턴 인식 (Pattern Recognition)
- 이미지 분류, 필기체 인식, 얼굴 인식 등
- 데이터 군집화 (Clustering Analysis)
- 고객 세분화, 생물 정보학(Bioinformatics) 등
- 추천 시스템 (Recommendation System)
- 사용자 행동 데이터를 학습하여 개인화된 추천 제공
- 이상 탐지 (Anomaly Detection)
- 금융 사기 탐지, 네트워크 보안 분석 등
- 의료 데이터 분석 (Medical Data Analysis)
- 질병 분류, 유전자 데이터 분석
6. SOM vs. 다른 군집 분석 기법 비교
| 기법 | 학습 방식 | 주요 특징 | 적용 분야 |
|---|---|---|---|
| K-means | 비지도 학습 | 고정된 K개의 중심 설정 | 일반적인 군집 분석 |
| SOM | 비지도 학습 | 데이터 시각화 및 군집화 가능 | 패턴 분석, 시각화 |
| PCA | 차원 축소 | 선형 변환 기반 | 데이터 차원 축소 |
| DBSCAN | 밀도 기반 군집화 | 밀도가 높은 영역을 군집화 | 이상 탐지, 공간 데이터 분석 |
7. Python을 활용한 SOM 예제
from minisom import MiniSom
import numpy as np
import matplotlib.pyplot as plt
# 데이터 생성
data = np.random.rand(100, 3) # 100개의 3차원 데이터
# SOM 설정 (10x10 격자, 3차원 입력)
som = MiniSom(x=10, y=10, input_len=3, sigma=1.0, learning_rate=0.5)
som.random_weights_init(data)
som.train_random(data, 1000) # 1000번 반복 학습
# 시각화
plt.figure(figsize=(6, 6))
for x, t in zip(data, range(len(data))):
w = som.winner(x) # BMU 찾기
plt.text(w[0], w[1], str(t), ha='center', va='center')
plt.title("SOM 군집화 결과")
plt.show()8. SOM과 신경망 분석 기법의 차이점
| 구분 | SOM (Self-Organizing Map) | 일반 신경망 (Artificial Neural Networks) |
|---|---|---|
| 학습 방식 | 비지도 학습 (Unsupervised Learning) | 지도 학습 (Supervised Learning) |
| 출력 형태 | 군집(Clustering) 형태의 2D/3D 격자 맵 | 특정 값 예측 (Classification, Regression) |
| 가중치 업데이트 | 경쟁 학습(Competitive Learning) 기반, BMU와 이웃 뉴런 업데이트 | 오차 역전파(Backpropagation) 사용 |
| 활용 목적 | 데이터 군집화, 차원 축소, 패턴 분석 | 이미지 인식, 음성 인식, NLP 등 |
| 대표 알고리즘 | Kohonen SOM | MLP, CNN, RNN, LSTM |
| 네트워크 구조 | 입력층 + 경쟁층 (1~2개 층) | 입력층 + 은닉층 다수 + 출력층 |
🔹 핵심 차이점 정리
- SOM은 지도 학습이 아닌 “비지도 학습”을 수행 → 라벨이 필요 없음
- SOM은 군집화(Clustering) 목적 → 신경망은 일반적으로 예측/분류를 수행
- SOM은 경쟁 학습을 사용하여 가중치를 조정 → 일반 신경망은 역전파(Backpropagation)를 사용
- SOM은 저차원 시각화(2D 격자) → 일반 신경망은 복잡한 다층 구조 가능
- SOM은 데이터의 패턴을 발견하는 데 강점 → 일반 신경망은 복잡한 관계 학습 가능
9. SOM의 한계점
- 고차원 데이터의 시각화는 2D 또는 3D로 제한됨
- BMU 매칭 방식이 K-means보다 계산량이 많음
- 초기 가중치 설정에 따라 학습 결과가 달라질 수 있음
- 하이퍼파라미터(격자 크기, 학습률, 이웃 함수) 설정이 중요
🔹 결론
SOM은 비지도 학습을 통해 데이터의 패턴을 스스로 학습하고 군집화하는 강력한 기법입니다. 특히, 고차원 데이터를 2D로 변환하여 직관적인 시각화를 제공한다는 점에서 많은 응용이 가능합니다. 하지만 하이퍼파라미터 설정과 계산량이 많다는 점을 고려해야 합니다.
※ 참고로 본 내용은 정보관리기술사 134회 4교시에 출제된 Topic입니다.
6. 군집분석 기법인 SOM(Self-Organizing Map)에 대하여 설명하시오.
가. SOM 정의 및 특징
나. SOM 구성요소
다. SOM과 신경망 분석기법의 차이점
