릿지(Ridge)는 머신러닝과 통계에서 사용되는 릿지 회귀(Ridge Regression) 또는 릿지 정규화(Ridge Regularization) 를 의미합니다. 이는 선형 회귀(Linear Regression)의 일종으로, 과적합(Overfitting)을 방지하기 위해 가중치(Weight)에 패널티를 추가하는 방법입니다.
1. 릿지 회귀(Ridge Regression)란?
- 선형 회귀의 확장으로, 일반적인 선형 회귀는 최소제곱법(Ordinary Least Squares, OLS)을 사용하여 오차를 최소화하지만, 데이터가 많거나 다중 공선성(Multicollinearity)이 있는 경우 과적합이 발생할 수 있음.
- 이를 해결하기 위해 릿지 회귀는 L2 정규화(L2 Regularization) 를 적용하여 모델이 너무 복잡해지는 것을 방지함.
2. 릿지 회귀의 수식
릿지 회귀는 기존 선형 회귀에 L2 패널티를 추가한 형태입니다
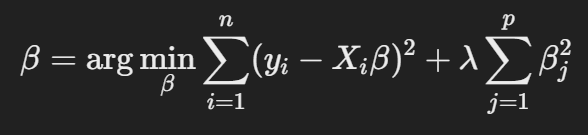
- 첫 번째 항: 일반적인 선형 회귀에서 사용하는 손실 함수 (MSE)
- 두 번째 항: 릿지 패널티(Regularization Term), 모델의 복잡도를 제어
- λ(람다): 정규화 강도를 조절하는 하이퍼파라미터
- λ가 클수록: 가중치가 작아지며 모델이 단순해짐 (규제 강함)
- λ가 작을수록: 선형 회귀와 비슷하게 동작함 (규제 약함)
3. 릿지 회귀의 특징
✅ 다중 공선성 해결
- 다중 공선성이 있는 데이터에서 선형 회귀를 적용하면 회귀 계수가 매우 불안정해짐.
- 릿지 회귀는 회귀 계수를 작게 만들어 다중 공선성 문제를 완화함.
✅ 변수 선택이 아닌 가중치 감소
- Lasso 회귀와 다르게 특정 변수의 계수를 완전히 0으로 만들지 않음.
- 즉, 모든 변수는 일정한 가중치를 가짐.
✅ λ 값 조절이 중요
- 너무 크면 모델이 너무 단순해지고(Underfitting), 너무 작으면 과적합 가능성이 있음.
4. 릿지 vs 라쏘(Lasso)
| 비교 항목 | 릿지 회귀 (Ridge) | 라쏘 회귀 (Lasso) |
|---|---|---|
| 정규화 방식 | L2 정규화 (제곱합) | L1 정규화 (절댓값 합) |
| 과적합 방지 | 가능 | 가능 |
| 계수 축소 | 모든 계수를 작게 만듦 | 일부 계수를 0으로 만듦(변수 선택 효과) |
| 다중 공선성 해결 | 효과적 | 효과적이지만 릿지보다 덜 안정적 |
| 변수 선택 기능 | 없음 | 있음 |
- 릿지는 모든 변수를 사용하면서 영향력을 조절하고,
- 라쏘는 일부 변수의 가중치를 0으로 만들어 변수 선택 기능이 있음.
5. 릿지 회귀 적용 예시 (Python 코드)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_regression
# 데이터 생성
X, y = make_regression(n_samples=100, n_features=1, noise=15, random_state=42)
# 데이터 스케일링
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 훈련/테스트 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)
# 릿지 회귀 모델 학습
ridge = Ridge(alpha=1.0) # λ = 1.0
ridge.fit(X_train, y_train)
# 예측값
y_pred = ridge.predict(X_test)
# 그래프 시각화
plt.scatter(X_test, y_test, color="blue", label="Actual")
plt.plot(X_test, y_pred, color="red", linewidth=2, label="Ridge Regression")
plt.legend()
plt.show()6. 릿지 회귀를 사용하는 경우
- 다중 공선성이 있는 데이터셋을 다룰 때
- 모델이 너무 복잡하여 과적합을 방지하려고 할 때
- 모든 변수를 유지하면서 가중치를 조절하고 싶을 때 (변수 선택보다는 영향력 조절)
7. 한 줄 요약
릿지 회귀(Ridge Regression) 는 선형 회귀의 일종으로 L2 정규화를 사용하여 과적합을 방지하고 다중 공선성 문제를 해결하는 기법입니다. 하지만 변수 선택 기능은 없으며, 모든 변수의 영향을 줄이는 방식으로 작동합니다.
